算法简介
B+树
B+Tree是在B-Tree基础上的一种优化,使其更适合实现外存储索引结构,InnoDB存储引擎就是用B+Tree实现其索引结构。
从上一节中的B-Tree结构图中可以看到每个节点中不仅包含数据的key值,还有data值。而每一个页的存储空间是有限的,如果data数据较大时将会导致每个节点(即一个页)能存储的key的数量很小,当存储的数据量很大时同样会导致B-Tree的深度较大,增大查询时的磁盘I/O次数,进而影响查询效率。在B+Tree中,所有数据记录节点都是按照键值大小顺序存放在同一层的叶子节点上,而非叶子节点上只存储key值信息,这样可以大大加大每个节点存储的key值数量,降低B+Tree的高度。
B+Tree相对于B-Tree有几点不同:
非叶子节点只存储键值信息。
所有叶子节点之间都有一个链指针。
数据记录都存放在叶子节点中。
节点分裂过程
在下图M=3中插入19,首先找到19的插入位置,插入;
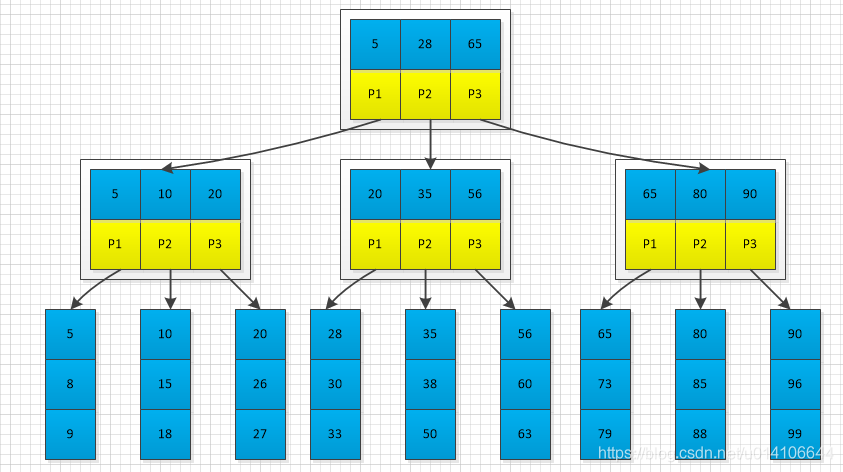
插入之后,出现节点已满
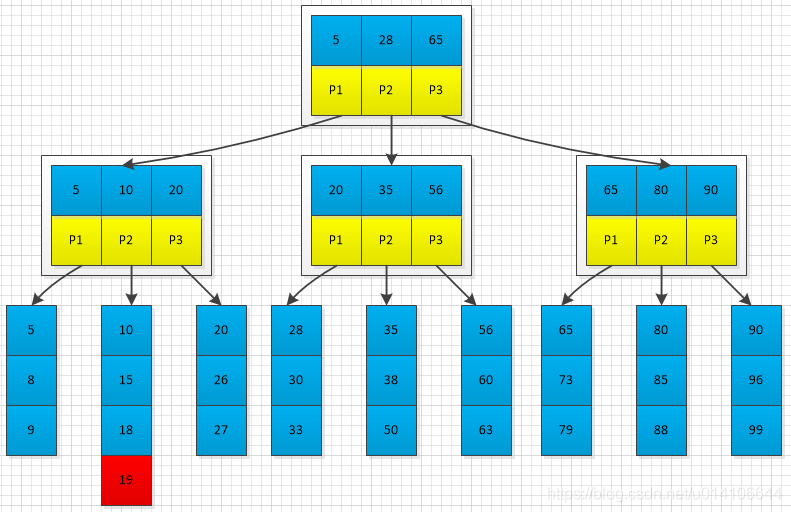
将已满节点进行分裂,将已满节点后M/2节点生成一个新节点,将新节点的第一个元素指向父节点;
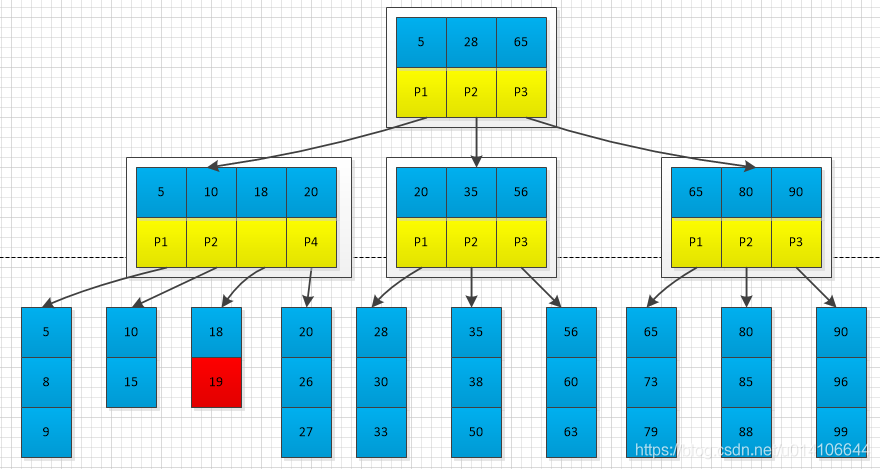
父节点出现已满,将父节点继续分裂
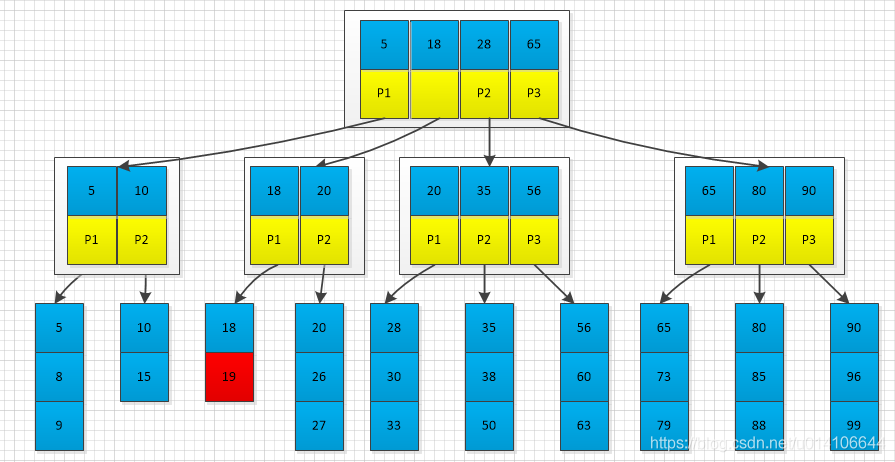
一直分裂,如果根节点已满,则需要分类根节点,此时树的高度增加
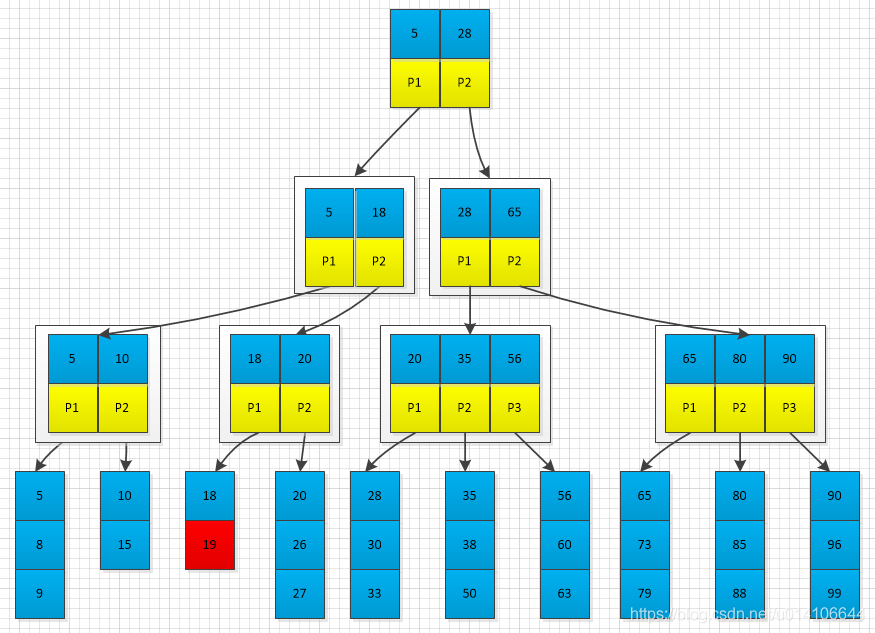
对于根节点分裂,新建一个节点 将旧根节点第一个元素以及分类节点第一个元素组合作为新的根节点。
1.1 节点的定义
public class BTree, Value> {
//参数M 定义每个节点的链接数
private static final int M = 4;
private Node root;
//树的高度 最底层为0 表示外部节点 根具有最大高度
private int height;
//键值对总数
private int n;
//节点数据结构定义
private static final class Node{
//值的数量
private int m;
private Entry[] children = new Entry[M];
private Node(int k){
m = k;
}
}
//节点内部每个数据项定义
private static class Entry{
private Comparable key;
private final Object val;
//下一个节点
private Node next;
public Entry(Comparable key, Object val, Node next){
this.key = key;
this.val = val;
this.next = next;
}
@Override
public String toString() {
StringBuilder builder = new StringBuilder();
builder.append("Entry [key=");
builder.append(key);
builder.append("]");
return builder.toString();
}
}
1.2节点的查询:
public Value get(Key key){
return search(root, key, height);
}
private Value search(Node x, Key key, int ht) {
Entry[] children = x.children;
//外部节点 这里使用顺序查找
//如果M很大 可以改成二分查找
if(ht == 0){
for(int j=0; j< x.m; j++){
if(equal(key, x.children[j].key))
return (Value)children[j].val;
}
}
//内部节点 寻找下一个节点
else{
for(int j=0; j< x.m; j++){
//最后一个节点 或者 插入值小于某个孩子节点值
if(j+1==x.m || less(key, x.children[j+1].key))
return search(x.children[j].next, key, ht-1);
}
}
return null;
}
1.3节点的插入:
public void put(Key key, Value val){
//插入后的节点 如果节点分裂,则返回分裂后产生的新节点
Node u = insert(root, key, val, height);
n++;
//根节点没有分裂 直接返回
if(u == null) return;
//分裂根节点
Node t = new Node(2);
//旧根节点第一个孩子 新分裂节点
t.children[0] = new Entry(root.children[0].key, null, root);
t.children[1] = new Entry(u.children[0].key, null, u);
root = t;
height++;
}
private Node insert(Node h, Key key, Value val, int ht) {
int j;
//新建待插入数据数据项
Entry t = new Entry(key, val, null);
// 外部节点 找到带插入的节点位置j
if(ht == 0){
for(j=0; j< h.m; j++){
if(less(key, h.children[j].key))
break;
}
}else{
//内部节点 找到合适的分支节点
for(j=0; j< h.m; j++){
if(j+1==h.m || less(key, h.children[j+1].key)){
Node u = insert(h.children[j++].next, key, val, ht-1);
if(u == null) return null;
t.key = u.children[0].key;
t.next = u;
break;
}
}
}
//System.out.println(j + t.toString());
//j为带插入位置,将顺序数组j位置以后后移一位 将t插入
for(int i=h.m; i>j; i++){
h.children[i] = h.children[i-1];
}
System.out.println(j + t.toString());
h.children[j] = t;
h.m++;
if(h.m < M) return null;
//如果节点已满 则执行分类操作
else return split(h);
}
private Node split(Node h) {
//将已满节点h的后一般M/2节点分裂到新节点并返回
Node t = new Node(M/2);
h.m = M / 2;
for(int j=0; j< M/2; j++)
t.children[j] = h.children[M/2+j];
return t;
}
1.4节点的分裂
public void put(Key key, Value val){
//插入后的节点 如果节点分裂,则返回分裂后产生的新节点
Node u = insert(root, key, val, height);
n++;
//根节点没有分裂 直接返回
if(u == null) return;
//分裂根节点
Node t = new Node(2);
//旧根节点第一个孩子 新分裂节点第一个孩子组成新节点作为根
t.children[0] = new Entry(root.children[0].key, null, root);
t.children[1] = new Entry(u.children[0].key, null, u);
root = t;
height++;
}