算法简介
红黑树
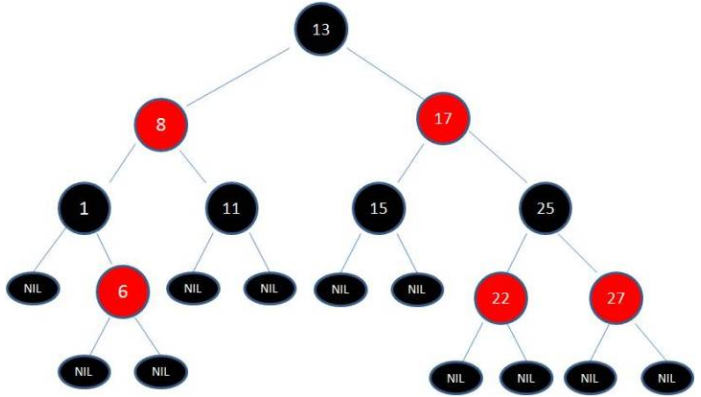
红黑树是基于二叉排序树的升级版,具有以下特性(自平衡特性):
1:节点非红色即黑色
2:根节点为黑色的
3:叶子结点都是黑色的空结点(nil结点)
4:每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)(就是红色后要接一个黑色的,黑色后一般也要接一个红色的)
5:从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点(左子树和右子树的黑结点的层数是相等)
红黑树从根节点到叶子节点的最长路径不会超过最短路径的两倍。
插入的节点都是红色的节点
红黑树的基本操作是添加、删除。在对红黑树进行添加或删除之后,都会用到旋转方法。为什么呢?道理很简单,添加或删除红黑树中的节点之后,红黑树就发生了变化,可能不满足红黑树的5条性质,也就不再是一颗红黑树了,而是一颗普通的树。而通过旋转,可以使这颗树重新成为红黑树。简单点说,旋转的目的是让树保持红黑树的特性。 旋转包括两种:左旋 和 右旋。
左旋:(以x为节点进行左旋)

对x进行左旋,意味着,将“x的右孩子”设为“x的父亲节点”;即,将 x变成了一个左节点(x成了为z的左孩子)!。 因此,左旋中的“左”,意味着“被旋转的节点将变成一个左节点”。
右旋:(以x为节点进行右旋)

对x进行右旋,意味着,将“x的左孩子”设为“x的父亲节点”;即,将 x变成了一个右节点(x成了为y的右孩子)! 因此,右旋中的“右”,意味着“被旋转的节点将变成一个右节点”。
1.1 左旋伪代码
LEFT-ROTATE(T, x)
01 y ← right[x]
// 前提:这里假设x的右孩子为y。下面开始正式操作
02 right[x] ← left[y]
// 将 “y的左孩子” 设为 “x的右孩子”,即 将β设为x的右孩子
03 p[left[y]] ← x
// 将 “x” 设为 “y的左孩子的父亲”,即 将β的父亲设为x
04 p[y] ← p[x]
// 将 “x的父亲” 设为 “y的父亲”
05 if p[x] = nil[T]
06 then root[T] ← y
// 情况1:如果 “x的父亲” 是空节点,则将y设为根节点
07 else if x = left[p[x]]
08 then left[p[x]] ← y
// 情况2:如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子”
09 else right[p[x]] ← y
// 情况3:(x是它父节点的右孩子) 将y设为“x的父节点的右孩子”
10 left[y] ← x // 将 “x” 设为 “y的左孩子”
11 p[x] ← y // 将 “x的父节点” 设为 “y”
1.2 右旋伪代码
RB-INSERT(T, z)
01 y ← nil[T] // 新建节点“y”,将y设为空节点。
02 x ← root[T] // 设“红黑树T”的根节点为“x”
03 while x ≠ nil[T] // 找出要插入的节点“z”在二叉树T中的位置“y”
04 do y ← x
05 if key[z] < key[x]
06 then x ← left[x]
07 else x ← right[x]
08 p[z] ← y // 设置 “z的父亲” 为 “y”
09 if y = nil[T]
10 then root[T] ← z
// 情况1:若y是空节点,则将z设为根
11 else if key[z] < key[y]
12 then left[y] ← z
// 情况2:若“z所包含的值” < “y所包含的值”,则将z设为“y的左孩子”
13 else right[y] ← z
// 情况3:(“z所包含的值” >= “y所包含的值”)将z设为“y的右孩子”
14 left[z] ← nil[T] // z的左孩子设为空
15 right[z] ← nil[T]
// z的右孩子设为空。至此,已经完成将“节点z插入到二叉树”中了。
16 color[z] ← RED // 将z着色为“红色”
17 RB-INSERT-FIXUP(T, z)
// 通过RB-INSERT-FIXUP对红黑树的节点进行颜色修改以及旋转,让树T仍然是一颗红黑树
2 插入伪代码
RB-INSERT(T, z)
01 y ← nil[T] // 新建节点“y”,将y设为空节点。
02 x ← root[T] // 设“红黑树T”的根节点为“x”
03 while x ≠ nil[T]
// 找出要插入的节点“z”在二叉树T中的位置“y”
04 do y ← x
05 if key[z] < key[x]
06 then x ← left[x]
07 else x ← right[x]
08 p[z] ← y // 设置 “z的父亲” 为 “y”
09 if y = nil[T]
10 then root[T] ← z // 情况1:若y是空节点,则将z设为根
11 else if key[z] < key[y]
12 then left[y] ← z
// 情况2:若“z所包含的值” < “y所包含的值”,则将z设为“y的左孩子”
13 else right[y] ← z
// 情况3:(“z所包含的值” >= “y所包含的值”)将z设为“y的右孩子”
14 left[z] ← nil[T] // z的左孩子设为空
15 right[z] ← nil[T]
// z的右孩子设为空。至此,已经完成将“节点z插入到二叉树”中了。
16 color[z] ← RED // 将z着色为“红色”
17 RB-INSERT-FIXUP(T, z)
// 通过RB-INSERT-FIXUP对红黑树的节点进行颜色修改以及旋转,让树T仍然是一颗红黑树
3 删除伪代码
RB-INSERT-FIXUP(T, z)
01 while color[p[z]] = RED
// 若“当前节点(z)的父节点是红色”,则进行以下处理。
02 do if p[z] = left[p[p[z]]]
// 若“z的父节点”是“z的祖父节点的左孩子”,则进行以下处理。
03 then y ← right[p[p[z]]]
// 将y设置为“z的叔叔节点(z的祖父节点的右孩子)”
04 if color[y] = RED
05 then color[p[z]] ← BLACK
06 color[y] ← BLACK
07 color[p[p[z]]] ← RED
08 z ← p[p[z]]
09 else if z = right[p[z]]
10 then z ← p[z]
11 LEFT-ROTATE(T, z)
12 color[p[z]] ← BLACK
13 color[p[p[z]]] ← RED
14 RIGHT-ROTATE(T, p[p[z]])
15 else (same as then clause with "right" and "left" exchanged)
16 color[root[T]] ← BLACK