Make It Easy

伸展树

Splaying是Splay Tree中的基本操作，为了让被查询的条目更接近树根，Splay Tree使用了树的旋转操作，同时保证二叉排序树的性质不变。

Splaying的操作受以下三种因素影响：

节点x是父节点p的左孩子还是右孩子

节点p是不是根节点，如果不是

节点p是父节点g的左孩子还是右孩子

同时有三种基本操作：

Zig Step

当p为根节点时，进行zip step操作。 当x是p的左孩子时，对x右旋； 当x是p的右孩子时，对x左旋。

Zig-Zig Step

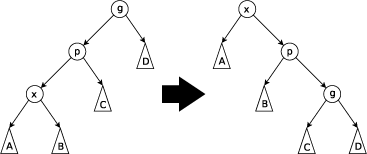
当p不是根节点，且x和p同为左孩子或右孩子时进行Zig-Zig操作。 当x和p同为左孩子时，依次将p和x右旋； 当x和p同为右孩子时，依次将p和x左旋。

Zig-Zag Step

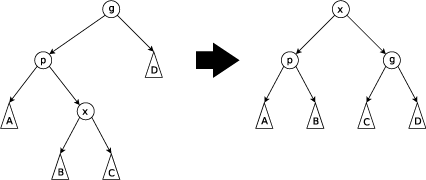
当p不是根节点，且x和p不同为左孩子或右孩子时，进行Zig-Zag操作。 当p为左孩子，x为右孩子时，将x左旋后再右旋。 当p为右孩子，x为左孩子时，将x右旋后再左旋。

Splay Tree可以方便的解决一些区间问题，根据不同形状二叉树先序遍历结果不变的特性，可以将区间按顺序建二叉查找树。 每次自下而上的一套splay都可以将x移动到根节点的位置，利用这个特性，可以方便的利用Lazy的思想进行区间操作。 对于每个节点记录size，代表子树中节点的数目，这样就可以很方便地查找区间中的第k小或第k大元素。 对于一段要处理的区间[x, y]，首先splay x-1到root，再splay y+1到root的右孩子，这时root的右孩子的左孩子对应子树就是整个区间。 这样，大部分区间问题都可以很方便的解决， 操作同样也适用于一个或多个条目的添加或删除，和区间的移动。

1.1	节点的定义
template < class T>
class SplayTreeNode{
    public:
        T key;                // 关键字(键值)
        SplayTreeNode *left;    // 左孩子
        SplayTreeNode *right;    // 右孩子


        SplayTreeNode():left(NULL),right(NULL) {}

        SplayTreeNode(T value, SplayTreeNode *l, SplayTreeNode *r):
            key(value), left(l),right(r) {}
};
1.2 伸展树：
template < class T>
class SplayTree {
    private:
        SplayTreeNode< T> *mRoot;    // 根结点
    public:
        SplayTree();
        ~SplayTree();
        // 前序遍历"伸展树"
        void preOrder();
        // 中序遍历"伸展树"
        void inOrder();
        // 后序遍历"伸展树"
        void postOrder();
        // (递归实现)查找"伸展树"中键值为key的节点
        SplayTreeNode< T>* search(T key);
        // (非递归实现)查找"伸展树"中键值为key的节点
        SplayTreeNode< T>* iterativeSearch(T key);
        // 查找最小结点：返回最小结点的键值。
        T minimum();
        // 查找最大结点：返回最大结点的键值。
        T maximum();
        // 旋转key对应的节点为根节点，并返回值为根节点。
        void splay(T key);
        // 将结点(key为节点键值)插入到伸展树中
        void insert(T key);
        // 删除结点(key为节点键值)
        void remove(T key);
        // 销毁伸展树
        void destroy();
        // 打印伸展树
        void print();
    private:
        // 前序遍历"伸展树"
        void preOrder(SplayTreeNode< T>* tree) const;
        // 中序遍历"伸展树"
        void inOrder(SplayTreeNode< T>* tree) const;
        // 后序遍历"伸展树"
        void postOrder(SplayTreeNode< T>* tree) const;
        // (递归实现)查找"伸展树x"中键值为key的节点
        SplayTreeNode< T>* search(SplayTreeNode< T>* x, T key) const;
        // (非递归实现)查找"伸展树x"中键值为key的节点
        SplayTreeNode< T>* iterativeSearch(SplayTreeNode< T>* x, T key) const;
        // 查找最小结点：返回tree为根结点的伸展树的最小结点。
        SplayTreeNode< T>* minimum(SplayTreeNode< T>* tree);
        // 查找最大结点：返回tree为根结点的伸展树的最大结点。
        SplayTreeNode< T>* maximum(SplayTreeNode< T>* tree);
        // 旋转key对应的节点为根节点，并返回值为根节点。
        SplayTreeNode< T>* splay(SplayTreeNode< T>* tree, T key);

        // 将结点(z)插入到伸展树(tree)中
        SplayTreeNode< T>* insert(SplayTreeNode< T>* &tree, SplayTreeNode< T>* z);

        // 删除伸展树(tree)中的结点(键值为key)，并返回被删除的结点
        SplayTreeNode< T>* remove(SplayTreeNode< T>* &tree, T key);

        // 销毁伸展树
        void destroy(SplayTreeNode< T>* &tree);

        // 打印伸展树
        void print(SplayTreeNode< T>* tree, T key, int direction);
};
2 旋转
/*
 * 旋转key对应的节点为根节点，并返回值为根节点。
 * 注意：
 *   (a)：伸展树中存在"键值为key的节点"。
 *          将"键值为key的节点"旋转为根节点。
 *   (b)：伸展树中不存在"键值为key的节点"，并且key < tree->key。
 *      b-1 "键值为key的节点"的前驱节点存在的话，将"键值为key的节点"的前驱节点旋转为根节点。
 *      b-2 "键值为key的节点"的前驱节点存在的话，则意味着，key比树中任何键值都小，那么此时，将最小节点旋转为根节点。
 *   (c)：伸展树中不存在"键值为key的节点"，并且key > tree->key。
 *      c-1 "键值为key的节点"的后继节点存在的话，将"键值为key的节点"的后继节点旋转为根节点。
 *      c-2 "键值为key的节点"的后继节点不存在的话，则意味着，key比树中任何键值都大，那么此时，将最大节点旋转为根节点。
 */

template < class T>
SplayTreeNode< T>* SplayTree< T>::splay(SplayTreeNode< T>* tree, T key)
{
    SplayTreeNode< T> N, *l, *r, *c;

    if (tree == NULL)
        return tree;

    N.left = N.right = NULL;
    l = r = & N;
    for (;;)
    {
        if (key < tree->key)
        {
            if (tree->left == NULL)
                break;
            if (key < tree->left->key)
            {
                c = tree->left;                           /* rotate right */
                tree->left = c->right;
                c->right = tree;
                tree = c;
                if (tree->left == NULL)
                    break;
            }
            r->left = tree;                     /* link right */
            r = tree;
            tree = tree->left;
        }
        else if (key > tree->key)
        {
            if (tree->right == NULL)
                break;
            if (key > tree->right->key)
            {
                c = tree->right;           	  /* rotate left */
                tree->right = c->left;
                c->left = tree;
                tree = c;
                if (tree->right == NULL)
                    break;
            }
            l->right = tree;         		/* link left */
            l = tree;
            tree = tree->right;
        }
        else
        {
            break;
        }
    }

    l->right = tree->left;            		  /* assemble */
    r->left = tree->right;
    tree->left = N.right;
    tree->right = N.left;

    return tree;
}

template < class T>
void SplayTree< T>::splay(T key)
{
    mRoot = splay(mRoot, key);
}
3 节点的插入
/*
 * 将结点插入到伸展树中，并返回根节点
 *
 * 参数说明：
 *     tree 伸展树的根结点
 *     key 插入的结点的键值
 * 返回值：
 *     根节点
 */
template < class T>
SplayTreeNode< T>* SplayTree< T>::insert(SplayTreeNode< T>* &tree, SplayTreeNode< T>* z)
{
    SplayTreeNode< T> *y = NULL;
    SplayTreeNode< T> *x = tree;

    // 查找z的插入位置
    while (x != NULL)
    {
        y = x;
        if (z->key < x->key)
            x = x->left;
        else if (z->key > x->key)
            x = x->right;
        else
        {
            cout << "不允许插入相同节点(" << z->key << ")!" << endl;
            delete z;
            return tree;
        }
    }

    if (y==NULL)
        tree = z;
    else if (z->key < y->key)
        y->left = z;
    else
        y->right = z;

    return tree;
}

template < class T>
void SplayTree< T>::insert(T key)
{
    SplayTreeNode< T> *z=NULL;

    // 如果新建结点失败，则返回。
    if ((z=new SplayTreeNode< T>(key,NULL,NULL)) == NULL)
        return ;

    // 插入节点
    mRoot = insert(mRoot, z);
    // 将节点(key)旋转为根节点
    mRoot = splay(mRoot, key);
}
4 节点的删除
/*
 * 删除结点(节点的键值为key)，返回根节点
 *
 * 参数说明：
 *     tree 伸展树的根结点
 *     key 待删除结点的键值
 * 返回值：
 *     根节点
 */
template < class T>
SplayTreeNode< T>* SplayTree< T>::remove(SplayTreeNode< T>* &tree, T key)
{
    SplayTreeNode< T> *x;

    if (tree == NULL)
        return NULL;

    // 查找键值为key的节点，找不到的话直接返回。
    if (search(tree, key) == NULL)
        return tree;

    // 将key对应的节点旋转为根节点。
    tree = splay(tree, key);

    if (tree->left != NULL)
    {
        // 将"tree的前驱节点"旋转为根节点
        x = splay(tree->left, key);
        // 移除tree节点
        x->right = tree->right;
    }
    else
        x = tree->right;

    delete tree;

    return x;

}

template < class T>
void SplayTree< T>::remove(T key)
{
    mRoot = remove(mRoot, key);
}